Important Topics To Be Covered For JEE Mains And Adv.
- Concept Of Direction Cosines and Direction Ratios.
- Straight Lines in 3D.
- Planes.
Concept of Direction Cosines (DC) and Direction Ratio (DR)
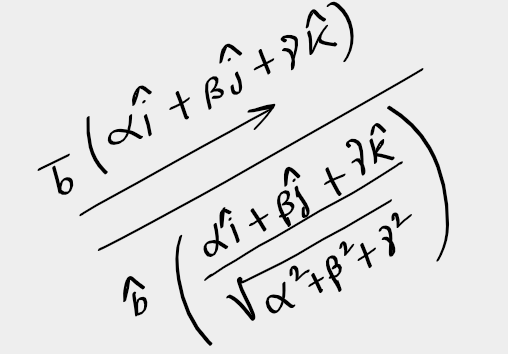
Here, (α,β,γ) are DR of line.
We can write it as DR of this line proportional to (α,β,γ) as it can be any multiple.
(\frac{\alpha}{\sqrt{\alpha^2+\beta^2+\gamma^2}}, \frac{\beta}{\sqrt{\alpha^2+\beta^2+\gamma^2}}, \frac{\gamma}{\sqrt{\alpha^2+\beta^2+\gamma^2}})
are DC of line.
Direction Cosine:-
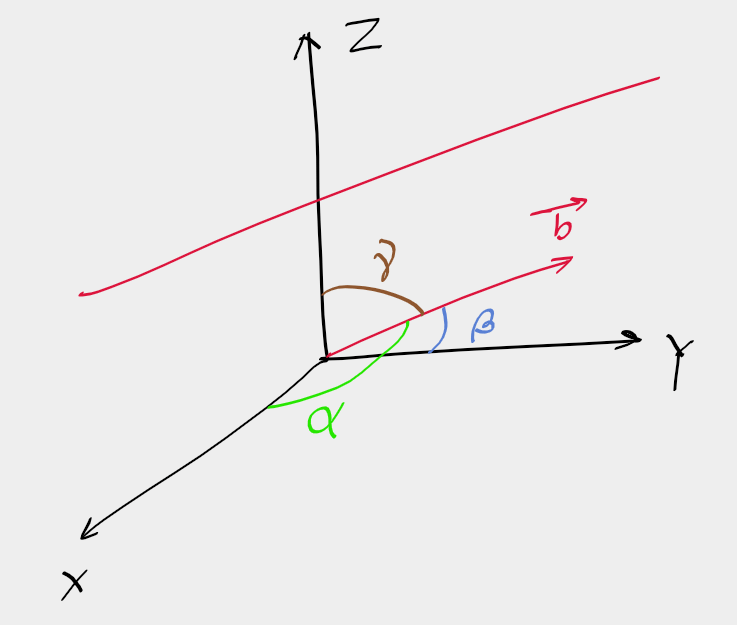
Vector b, which is parallel to the given line making α,β,γ angles with the X, Y and Z axes respectively, and the triplet cosα, cosβ, cosγ are called DC of this line.
\begin{aligned} & \hat{b}=(\cos \alpha) \hat{i}+(\cos \beta) \hat{j}+(\cos \gamma) \hat{k} \\ & \hat{b}=l \hat{i}+m \hat{j}+n \hat{k} \end{aligned}
\begin{aligned} \quad|\hat{b}|=1 \end{aligned}
\begin{aligned} \sqrt{l^2+m^2+n^2}=1 \end{aligned}
\begin{aligned} l^2+m^2+n^2=1 \end{aligned}
\begin{aligned} \cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1 \end{aligned}
Examples:
1. DC of X-axis are ±(1 , 0, 0)
DC of Y- axis are ±(0 , 1, 0)
DC of Z- axis are ±(0 , 0, 1)
2. If |a| = 5 and DC of vector a are ( 1/root2 , -1/root2 , 0 ) the vector a is:-
\begin{aligned} \frac{\bar{a}}{|\bar{a}|} & =\hat{a} \\ \bar{a} =|\vec{a}| \hat{a} \ & =5\left(\frac{i}{\sqrt{2}}-\frac{j}{\sqrt{2}}\right) \end{aligned}
3. The DC’s of a line equally inclined to the axes are :
l=m=n=x (say)
x2 + x2 + x2 = 1
so, x= ±1/root3
\begin{aligned} ± \left(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right) \end{aligned}
4. The DC of any normal to the XZ plane are : ±(0 , 1, 0)
The DC of any normal to the YZ plane are : ±(1 , 0, 0)
The DC of any normal to the XY plane are : ±(0 , 0, 1)
Angles between two lines in 3D :-
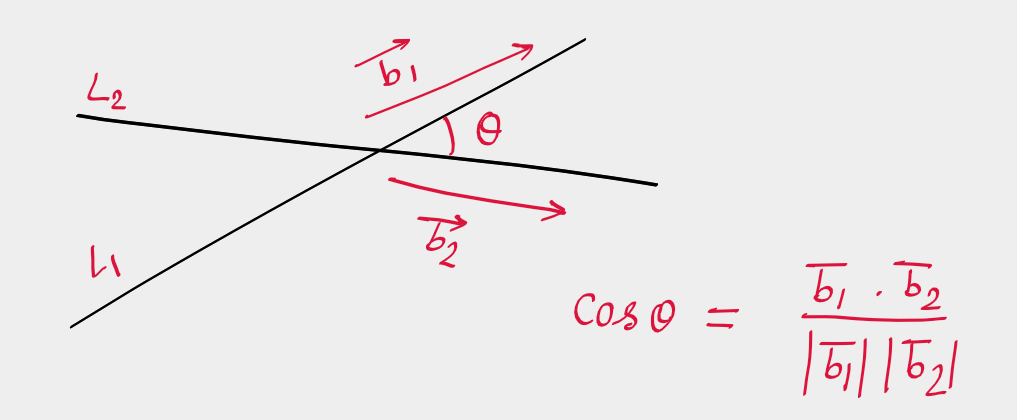
Angle between two lines is the angle between vectors parallel to these lines.
Straight Lines in 3D :-
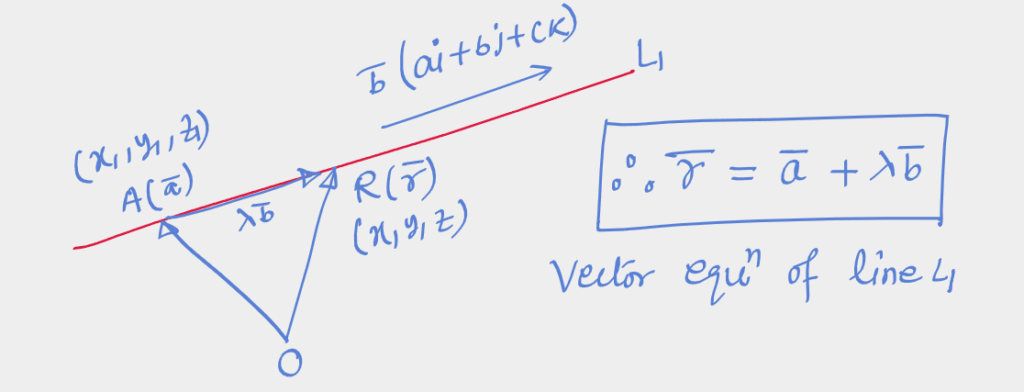
\begin{aligned} & \bar{r}=\bar{a}+\lambda \bar{b} \\ & x{i}+y{j}+z{k}=x_{1} i+y_{1} j+z_{1} k+\lambda(a i+b j+c k) \\ & \Rightarrow x \hat{i}+y \hat{j}+z \hat{k}=\left(x_{1}+\lambda a\right) \hat{i}+\left(y_{1}+\lambda b\right) \hat{j}+\left(z_{1}+\lambda c\right) \hat{k} \\ & \begin{array}{l|l|l} x=x_{1}+\lambda a & y=y_{1}+\lambda b & z=z_{1}+\lambda c \\ \frac{x-x_{1}}{a}=\lambda & \frac{y-y_{1}}{b}=\lambda & \frac{z-z_{1}}{c}=\lambda \end{array} \\ & \frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}=\lambda ————— (1) \end{aligned}
Where DR of vector parallel to the given line ∝( a, b, c ), ( x1 , y1 , z1 ) is a point on the given line and ( x, y, z ) is any arbitrary point on the given line.
Equation (1) is the cartesian form of the line L1.
Cartesian Equations : –
(1) Line passes through a point ( 1, 1, -2 ) and parallel to the vector i+2j+3k
\begin{aligned} \frac{x-1}{1}=\frac{y-1}{2}=\frac{z+2}{3} \end{aligned}
(2) Line passes through a point ( 1, 1, -2 ) and DR of the vector parallel to the line ∝( 1, 2, 3 )
\begin{aligned} \frac{x-1}{1}=\frac{y-1}{2}=\frac{z+2}{3} \end{aligned}
(3) Line passes through a point ( 1, 1, -2 ) and DC of the vector parallel to the line ( 1/√5 , 2/√5, 3/√5 )
\begin{aligned} \frac{x-1}{1/√5}=\frac{y-1}{2/√5}=\frac{z+2}{3/√5} \end{aligned}
(4) Equation of Y-axis in 3D :
\begin{aligned} \frac{x-0}{0}=\frac{y-0}{1}=\frac{z-0}{0} \end{aligned}
(5) Equation of X-axis in 3D :
\begin{aligned} \frac{x-0}{1}=\frac{y-0}{0}=\frac{z-0}{0} \end{aligned}
(6) Equation of Z-axis in 3D :
\begin{aligned} \frac{x-0}{0}=\frac{y-0}{0}=\frac{z-0}{1} \end{aligned}
Standard Varieties of Lines in 3D :-
\begin{aligned} & (a) \ \ 6 x-2=3 y+1=2 z-1 \\ & \frac{x-\frac{1}{3}}{\frac{1}{6}}=\frac{y+\frac{1}{3}}{\frac{1}{3}}=\frac{z-\frac{1}{2}}{\frac{1}{2}} \end{aligned}
\begin{aligned} (b) \ \frac{x-2}{2}=\frac{2 y-5}{-3} ; \quad z=-1 \\ \frac{x-2}{2}=\frac{2 y-5}{-3}=\frac{z+1}{0} \\ \frac{x-2}{2}=\frac{y-5 / 2}{-3 / 2}=\frac{z+1}{0} \ \end{aligned}
(Here z=-1 is constant and this line is perpendicular to z-axis. So, δ=90 degrees and cos 90=0. So, DC is zero.)
\begin{aligned} (c) \ \ x=2 y+3 ; z=y-4 \\ \frac{x-3}{2}=y=z+4 \\ \frac{x-3}{2}=\frac{y-0}{1}=\frac{z+4}{1} \end{aligned}
Q: The lines x=ay+ b ; z=cy+ d and x=a’y+ b’ ; z=c’y+ d’ are perpendicular if
(a) aa’+cc’+1=0
(b) ac’+a’c+1=0
(c) ac+a’c’+1=0
(d) aa’+cc’=1
Solution:
x=ay+ b ; z=cy+ d
Standard format is
\begin{aligned} \frac{x-b}{a}=\frac{y-0}{1}=\frac{z-d}{c} \end{aligned}
\begin{aligned} \bar{r_1}=a \hat{i}+\hat{j}+c \hat{k} \end{aligned}
Similarly,
x=a’y+ b’ ; z=c’y+ d’
Standard format is
\begin{aligned} \frac{x-b^{\prime}}{a^{\prime}}=\frac{y-0}{1}=\frac{z-d^{\prime}}{c^{\prime}} \end{aligned}
\begin{aligned} \bar{r_2}={a^{\prime}} \hat{i}+\hat{j}+{c^{\prime}} \hat{k} \end{aligned}
Since these two lines are perpendicular so,
\begin{aligned} \bar{r_1}.\bar{r_2}=0 \end{aligned}
\begin{aligned} \ (a \hat{i}+\hat{j}+c \hat{k}).({a^{\prime}} \hat{i}+\hat{j}+{c^{\prime}} \hat{k}) =0\end{aligned}
\begin{aligned} \ a a^{\prime}+c c^{\prime}+1=0\end{aligned}