Let a, b, c be three vectors. Consider the following expressions, these are called scalar triple product of vectors a, b, c.
(\vec{a} \times \vec{b}) \cdot \vec{c} or [\vec{a}\ \vec{b}\ \vec{c}]
The above expression is also called Mixed product or Box product. Using permutation of three vectors in six different ways we get total twelve scalar products of vectors a, b, c by changing the position of dot and cross. Clearly all are scalar values.
\begin{array}{llllll} \vec{a} \times \vec{b} \cdot \vec{c} & \vec{b} \times \vec{c} \cdot \vec{a} & \vec{c} \times \vec{a} \cdot \vec{b} & \vec{a} \cdot \vec{b} \times \vec{c} & \vec{b} \cdot \vec{c} \times \vec{a} & \vec{c} \cdot \vec{a} \times \vec{b} \\ \vec{a} \times \vec{c} \cdot \vec{b} & \vec{b} \times \vec{a} \cdot \vec{c} & \vec{c} \times \vec{b} \cdot \vec{a} & \vec{a} \cdot \vec{c} \times \vec{b} & \vec{b} \cdot \vec{a} \times \vec{c} & \vec{c} \cdot \vec{b} \times \vec{a} \end{array}
(\vec{a} \times \vec{b}) \cdot \vec{c}=[\vec{a}\ \vec{b}\ \vec{c}]
This above notation takes note of the cyclic order of the vectors a, b, c (i.e., abc, bca,cab etc.) and disregards the position of dot and cross.
\begin{aligned} & {[\vec{a}\ \vec{b}\ \vec{c}]=[\vec{b}\ \vec{c}\ \vec{a}]=[\vec{c}\ \vec{a}\ \vec{b}]} \\ & =-[\vec{a}\ \vec{c}\ \vec{b}]=-[\vec{b}\ \vec{a}\ \vec{c}]=-[\vec{c}\ \vec{b}\ \vec{a}] \end{aligned}
In cartesian form,
\begin{aligned} & \vec{a}=a_{1} \hat{i}+a_{2} \hat{j}+a_{3} \hat{k} \\ & \vec{b}=b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k} \\ & \vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k} \end{aligned}
We have,
(\vec{a} \times \vec{b}) \cdot \vec{c}=\left|\begin{array}{lll}a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3}\end{array}\right|
Q1. For any three vectors a, b, c prove that a. (b x c) = (a x b) .c
Proof:\vec{a} \cdot(\vec{b} \times c)=\left|\begin{array}{lll}a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3}\end{array}\right|
(\vec{a} \times \vec{b}) \cdot \vec{c}=\left|\begin{array}{lll}c_{1} & c_{2} & c_{3} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3}\end{array}\right|=\left|\begin{array}{lll}a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3}\end{array}\right|=\vec{a} \cdot(\vec{b} \times c)
Here, two times rows are interchanging the position. So, ultimately same value it will provide. Hence proved.
Properties of the Box product:-
(1)\left[\begin{array}{lll}l \vec{a} & m \vec{b} & n \vec{c}\end{array}\right]=\operatorname{lmn}\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]
Proof:-
\begin{aligned} & \left|\begin{array}{lll}l a_1 & l a_2 & l a_3 \\ m b_1 & m b_2 & m b_3 \\ n c_1 & n c_2 & n c_3\end{array}\right|=\operatorname{lmn}\left|\begin{array}{lll}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right| & \\\ Therefore, \left[\begin{array}{lll}l \vec{a} & m \vec{b} & n \vec{c}\end{array}\right]=\operatorname{lmn}\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right] \ & \end{aligned}
(2)\left[\begin{array}{ccc}\vec{a}+\vec{b} & \vec{c} & \vec{d}\end{array}\right]=\left[\begin{array}{lll}\vec{a} & \vec{c} & \vec{d}\end{array}\right]+\left[\begin{array}{lll}\vec{b} & \vec{c} & \vec{d}\end{array}\right]
Proof:-
\begin{aligned} & (\vec{a}+\vec{b}) \cdot(\vec{c} \times \vec{d}) \\ & =\vec{a} \cdot(\vec{c} \times \vec{d})+\vec{b} \cdot(\vec{c} \times \vec{d}) \\ & =[\vec{a}\ \ \ \vec{c}\ \ \ \vec{d}]+\left[\begin{array}{lll} \vec{b} & \vec{c} & \vec{d} \end{array}\right] \end{aligned}
Accordingly \begin{aligned} & {\left[\begin{array}{lll} \vec{a}+\vec{b} & \vec{c}+\vec{d} & \vec{e} \end{array}\right] \text { and }} \\ & {\left[\begin{array}{lll} \vec{a}+\vec{b} & \vec{c}+d & \vec{e}+\vec{f} \end{array}\right]} \end{aligned}
will break into 4 and 8 scalar triple products respectively.
(3) The Scalar triple product of the three vectors a, b, c i.e., [ a b c ] is zero if and only if these three vectors are coplanar. Also, the scalar triple product is zero if any two of the three vectors are parallel(or collinear). And if a, b, c are mutually perpendicular vectors, then [ a b c ]=|a| |b| |c|. So for i, j, k it will be [ i j k ]=1.
Proof:- \begin{aligned} & \vec{a} \cdot(\vec{b} \times \vec{c})=0 \\ & =>\vec{a} \perp(\vec{b} \times \vec{c}) \end{aligned}
Here, vector a is perpendicular to (b x c) which means a is on the same plane as vector b and c i.e., a, b, c are coplanar.
(4)
[\vec{a}\ \vec{b}\ \vec{c}]^{2}=\left|\begin{array}{lll}\vec{a} \cdot \vec{a} & \vec{a} \cdot \vec{b} & \vec{a} \cdot \vec{c} \\ \vec{b} \cdot \vec{a} & \vec{b} \cdot \vec{b} & \vec{b} \cdot \vec{c} \\ \vec{c} \cdot \vec{a} & \vec{c} \cdot \vec{b} & \vec{c} \cdot \vec{c}\end{array}\right|
(5)
\left[\begin{array}{lll} \vec{a}+\vec{b} & \vec{b}+\vec{c} & \vec{c}+\vec{a} \end{array}\right]=2[\vec{a}\ \ \vec{b}\ \ \vec{c}]
(6)
\left[\begin{array}{lll}\vec{a} \times \vec{b} & \vec{b} \times \vec{c} & \vec{c} \times \vec{a}\end{array}\right]=\left[\begin{array}{ll}\vec{a}\ \ \vec{b}\ \ \vec{c} \end{array}\right] { }^{2}
(7)\left[\begin{array}{lll} \vec{a}-\vec{b} & \vec{b}-\vec{c} & \vec{c}-\vec{a} \end{array}\right]=0
(8) \left[\begin{array}{lll} \vec{a} & \vec{b}+\vec{c} & \vec{a}+\vec{b}+\vec{c} \end{array}\right]=0
Geometrical Significance of the Box Product :-
The magnitude of [ a b c] gives the volume of the parallelopiped whose coinitial edges are vectors a, b and c as shown in the diagram given below.
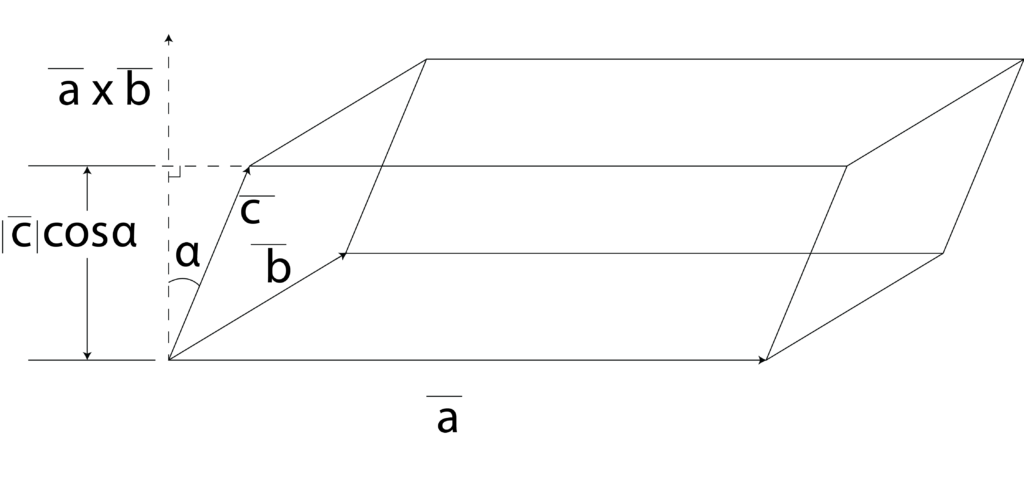
Volume = Base\ area \times Height\begin{aligned} & =(\vec{a} \times \vec{b}) \cdot|\bar{c}| \cos \alpha & =|(\vec{a} \times \vec{b}) \cdot \vec{c}| \end{aligned}
Reciprocal System of vectors:-
If a, b, c be three non-coplanar vectors such that [ a b c ] ≠ 0 then the below vectors
\vec{a}^{\prime}=\frac{\vec{b} \times \vec{c}}{[\vec{a}\ \vec{b}\ \vec{c}]},\ \ \vec{b}^{\prime}=\frac{\vec{c} \times \vec{a}}{[\vec{a}\ \vec{b}\ \vec{c}]},\ \ \vec{c}^{\prime}=\frac{\vec{a} \times \vec{b}}{[\vec{a}\ \vec{b}\ \vec{c}]}
Following are some important properties of reciprocal system of vectors.
(i)\ \vec{a} \cdot \vec{a}^{\prime}=\vec{b} \cdot \vec{b}^{\prime}=\vec{c} \cdot \vec{c}^{\prime}=1
(ii)\ \vec{a} \cdot \vec{b}^{\prime}=\vec{a} \cdot \vec{c}^{\prime}=\vec{b} \cdot \vec{c}^{\prime}=\vec{b} \cdot \vec{a^{\prime}}=\vec{c} \cdot \vec{a}{ }^{\prime}=\vec{c} \cdot \vec{b}^{\prime}=0
(iii)\ [\vec{a}\ \ \vec{b}\ \ \vec{c}]=\frac{1}{\left[\vec{a}^{\prime}\ \ \vec{b}^{\prime}\ \ \vec{c}^{\prime}\right]}
(iv)\ \vec{a} \cdot \vec{a}^{\prime}+\vec{b} \cdot \vec{b}^{\prime}+\vec{c} \cdot \vec{c}^{\prime}=3
Questions for practice
Q2. If the vectors ai + j + k, i +bj + k and i + j + ck (a, b, c ≠ 1) are coplanar, the find the value of the given expression \begin{aligned}\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}\end{aligned}
Answer:
\begin{aligned} & \left|\begin{array}{ccc} a & 1 & 1 \\ 1 & b & 1 \\ 1 & 1 & c \end{array}\right|=0 \\\\ & \left|\begin{array}{ccc} a & 1-a & 1-a \\ 1 & b-1 & 0 \\ 1 & 0 & c-1 \end{array}\right|=0\ \left(\begin{array}{l} c_{2} \rightarrow c_{2}-c_{1} \ c_{3} \rightarrow c_{3}-c_{1} \end{array}) \right. \\\\ \Rightarrow & a[(b-1)(c-1)]-(1-a)(c-1)+(1-a)(1-b)=0 \\ \Rightarrow & a(1-b)(1-c)+(1-a)(1-c)+(1-a)(1-b)=0 \\ \Rightarrow & \frac{a}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}=0 \\ \Rightarrow & \frac{1-(1-a)}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}=0 \\ \Rightarrow & \frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}=1 \end{aligned}
Q3. If vectors a=i+j+k, b=4i+3j+4k and c=i+αj+βk are linearly dependent and |c|=√ 3, then find α and β.
Answer:
Three vectors are linearly dependent means these three vectors are coplanar, we can write one vector in terms of other two.
\begin{aligned} & \sqrt{1+\alpha^{2}+\beta^{2}}=\sqrt{3} \\ \Rightarrow & \ \alpha^{2}+\beta^{2}=2 \\ & \left|\begin{array}{ccc} 1 & 1 & 1 \\ 4 & 3 & 4 \\ 1 & \alpha & \beta \end{array}\right|=0 \\\ \Rightarrow & (3 \beta-4 \alpha)-1(4 \beta-4)+1(4 \alpha-3)=0 \\\ \Rightarrow & 3 \beta-4 \alpha-4 \beta+4+4 \alpha-3=0 \\\ \Rightarrow & -\beta=-1 \quad \ \beta=1 \end{aligned}
Q4. If a, b, c are mutually perpendicular vectors of magnitude 1, 2, 3 units respectively. Find value of [ 2b-c 2c-a 2a-b ].
Answer:
Since, vectors a, b and c are mutually perpendicular vectors so,
{\left[\begin{array}{ccc} \bar{a} & \bar{b} & \bar{c} \end{array}\right]=|\vec{a}||\vec{b}||\vec{c}|=1 \times 2 \times 3=6 }
[2 \vec{b}-\vec{c} \ \ 2 \vec{c}-\vec{a} \ \ 2 \vec{a}-\vec{b}]
\begin{aligned} & =(2 \vec{b}-\vec{c}) \cdot ((2 \vec{c}-\vec{a}) \times(2 \vec{a}-\vec{b})) \\ & =(2 \vec{b}-\vec{c}) \cdot(4 \vec{c} \times \vec{a}-2 \vec{c} \times \vec{b}-\ 0+\vec{a} \times \vec{b}) \\ & =8 \cdot \vec{b} \cdot(\vec{c} \times \vec{a})-\vec{c} \cdot(\vec{a} \times \vec{b}) \\ & =7[\vec{a} \vec{b} \vec{c}]=7 \times 6=42 \end{aligned}
Q5. If the points A(a), B(b), C(c), D(d) are coplanar then prove that
[a b c]=[b c d] + [c a d] + [a b d] where a, b, c, d are position vectors of A, B, C and D respectively.
Answer:
If A(a), B(b), C(c), D(d) are four coplanar points then three vectors made by these four points should be coplanar.
\begin{aligned} & \overline{A B} \quad \overline{B C} \quad \overline{C D} \rightarrow \text { Coplanar } \\ & {[\bar{b}-\bar{a} \ \ \bar{c}-\bar{b} \ \ \bar{d}-\bar{c}]=0} \\ & {\left[\begin{array}{lll} \vec{b} & \vec{c} & \vec{d} \end{array}\right]+\left[\begin{array}{lll} \bar{b} & \vec{c} & -\vec{c} \end{array}\right]+\left[\begin{array}{lll} \vec{b} & -\vec{b} & \vec{d} \end{array}\right]+[\vec{b} \ -\vec{b} \ -\vec{c}]} +\left[\begin{array}{lll} -\vec{a} & \vec{c} & \vec{d} \end{array}\right]+\left[\begin{array}{ll} -\vec{a} & \vec{c} \ -\vec{c} \end{array}\right]+[-\vec{a}-\vec{b} \ \vec{d}]+[-\vec{a}-\vec{b}-\vec{c}]=0 \\ & \Rightarrow\left[\begin{array}{lll} \bar{b} & \bar{c} & \bar{d} \end{array}\right]-\left[\begin{array}{lll} \bar{a} & \bar{c} & d \end{array}\right]+\left[\begin{array}{lll} \vec{a} & \vec{b} & d \end{array}\right] -\left[\begin{array}{lll} \vec{a} & \vec{b} & \vec{c} \end{array}\right]=0 \end{aligned}
\Rightarrow\left[\begin{array}{lll} \vec{b} & \vec{c} & \vec{d} \end{array}\right]+\left[\begin{array}{lll} \vec{c} & \vec{a} & \vec{d} \end{array}\right]+\left[\begin{array}{lll} \vec{a} & \vec{b} & \vec{d} \end{array}\right] =\left[\begin{array}{lll} \vec{a} & \vec{b} & \vec{c} \end{array}\right]
Q6. Find the number of distinct real values of λ, for which the vectors -λ2 i +j +k, i -λ2 j +k and i +j -λ2 k are coplanar. [IIT JEE 2007]
Answer:
Given vectors are
-\lambda^{2} \hat{i}+\hat{j}+\hat{k}, \hat{i}-\lambda^{2} \hat{j}+\hat{k} \ and \ \hat{i}+\hat{j}-\lambda^{2} \hat{k}
Since vectors are coplanar
\Rightarrow\left|\begin{array}{ccc}-\lambda^{2} & 1 & 1 \\ 1 & -\lambda^{2} & 1 \\ 1 & 1 & -\lambda^{2}\end{array}\right|=0
\Rightarrow \quad-\lambda^{2}\left(\lambda^{4}-1\right)-1\left(-\lambda^{2}-1\right)+1\left(1+\lambda^{2}\right)=0
\Rightarrow-\lambda^{6}+3 \lambda^{2}+2=0
\Rightarrow\left(1+\lambda^{2}\right)^{2}\left(\lambda^{2}-2\right)=0
\Rightarrow \lambda= \pm \sqrt{2}, number \ of \ possible \ value =2
Q7. If the volume of a parallelopiped, whose coterminous edges are given by vectors a=i+j+nk, b=2i+4j-nk and c=i+nj+3k (n≥0) is 158 cubic units, then [JEE Main 2020]
(A) n=7 (B) b.c = 10 (C) n = 9 (D) a.c = 17
Answer:
\begin{aligned} & {\left[\begin{array}{ccc} \bar{a} & \bar{b} & \bar{c} \end{array}\right]=158 } \\\ &\left|\begin{array}{ccc} 1 & 1 & n \\ \ 2 & 4 & -n \\ 1 & n & 3 \end{array}\right|=158 \\ & \Rightarrow\left(12+n^{2}\right)-1(6+n)+n(2 n-4)=158 \\ & \Rightarrow n^{2}+12-6-n+2 n^{2}-4 n=158 \\ & \Rightarrow 3 n^{2}-5 n+6=158 \\ & \Rightarrow 3 n^{2}-5 n-152=0 \\ & \Rightarrow 3 n^{2}-24 n+19 n-152=0 \\ & \Rightarrow 3 n(n-8)+19(n-8)=0 \\ & \Rightarrow (n-8)(3 n+19)=0 \\ & n=8 \end{aligned}